Logistic growth ap calc bc – Logistic growth, a cornerstone of AP Calculus BC, unveils the fascinating patterns of population growth and decay. This mathematical model captures the dynamics of populations, from exponential growth to a carrying capacity limit, providing insights into real-world phenomena.
Delving into the logistic growth equation, we discover its parameters and their implications for population behavior. We’ll explore techniques for analyzing growth rates, carrying capacities, and inflection points, arming you with tools to decipher population trends.
Introduction to Logistic Growth: Logistic Growth Ap Calc Bc
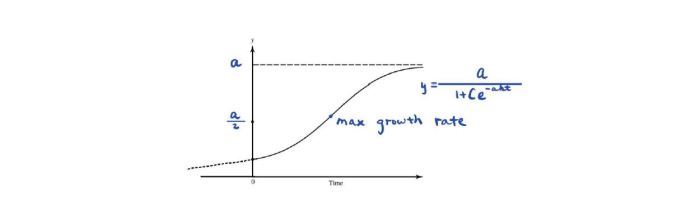
Logistic growth is a mathematical model that describes the growth of a population over time. It takes into account the carrying capacity of the environment, which is the maximum population size that can be sustained by the available resources.
Logistic growth is commonly observed in populations that experience limited resources, such as food, water, or shelter. As the population grows, the competition for these resources increases, which slows down the growth rate. Eventually, the population reaches a carrying capacity, where the birth rate and death rate are equal, and the population size stabilizes.
Examples of Logistic Growth in Real-World Applications
- Population growth of bacteria in a closed environment
- Spread of infectious diseases
- Growth of a company’s market share
- Adoption of new technologies
Mathematical Modeling of Logistic Growth
Logistic growth is a mathematical model that describes the growth of a population that has limited resources. The model is based on the assumption that the growth rate of the population is proportional to the population size and the amount of resources available.
Derivation of the Logistic Growth Equation
The logistic growth equation can be derived using differential equations. Let N( t) be the population size at time t. The growth rate of the population is given by the derivative of N( t) with respect to t:
dN/dt = rN(1 - N/K)
where ris the intrinsic growth rate and Kis the carrying capacity.
The intrinsic growth rate is the growth rate of the population when resources are unlimited. The carrying capacity is the maximum population size that can be supported by the available resources.
The logistic growth equation can be solved to obtain the following expression for N( t):
N(t) = K / (1 + e^(-rt + C))
where Cis a constant.
Parameters of the Logistic Growth Equation
The logistic growth equation has two parameters: the intrinsic growth rate ( r) and the carrying capacity ( K).
- Intrinsic growth rate (r): The intrinsic growth rate is the growth rate of the population when resources are unlimited. It is a positive constant.
- Carrying capacity (K): The carrying capacity is the maximum population size that can be supported by the available resources. It is a positive constant.
Analysis of Logistic Growth

The logistic growth equation provides valuable information about the characteristics of the growth curve. By analyzing the equation, we can determine the carrying capacity, growth rate, and inflection point, which are crucial parameters for understanding the dynamics of the population or system.
To analyze the logistic growth equation, we need to understand its key features.
Carrying Capacity
The carrying capacity ( K) represents the maximum population size that can be sustained by the environment. It is determined by factors such as resource availability, competition, and environmental conditions.
In the logistic growth equation:
N(t) = K / (1 + (K
- N(0))
- e^(-r
- t))
Kis the carrying capacity.
Growth Rate
The growth rate ( r) measures the rate at which the population increases or decreases. It is influenced by factors such as birth rates, death rates, and environmental factors.
Logistic growth in AP Calc BC is a crucial concept to grasp, and if you’re looking to test your understanding, be sure to check out the math models unit 3 quiz 1 . This quiz covers various aspects of logistic growth and will help you solidify your knowledge of this topic in AP Calc BC.
In the logistic growth equation:
N(t) = K / (1 + (K
- N(0))
- e^(-r
- t))
ris the growth rate.
Inflection Point
The inflection point is the point at which the growth curve changes from concave up to concave down. It represents the point where the population growth rate reaches its maximum.
The inflection point occurs when the population size is half of the carrying capacity ( N(t) = K/2).
Summary of Key Characteristics, Logistic growth ap calc bc
| Characteristic | Logistic Growth Equation |
|---|---|
| Carrying Capacity | K |
| Growth Rate | r |
| Inflection Point | N(t) = K/2 |
Applications in AP Calculus BC

Logistic growth is widely used in AP Calculus BC to model population growth and decay problems. It helps determine the carrying capacity of an environment, the rate of population change, and the time required for a population to reach a specific size.
Example Exam-Style Questions
Exam-style questions involving logistic growth typically require students to:
- Write the differential equation for a logistic growth model.
- Solve the differential equation to find the population function.
- Use the population function to analyze the population growth and decay.
For instance, a question might ask students to model the growth of a bacterial population that doubles every hour, assuming an initial population of 100 bacteria.
Extensions of Logistic Growth
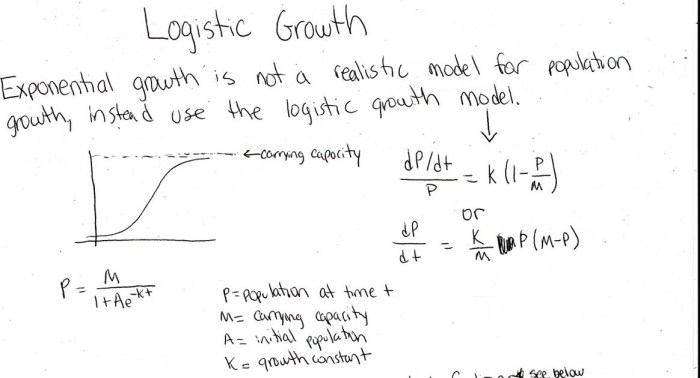
The logistic growth model is a versatile tool for capturing the dynamics of population growth and other phenomena that exhibit an initial period of rapid growth followed by a gradual leveling off. However, there are situations where the standard logistic equation may not adequately describe the observed growth pattern.
In such cases, extensions of the logistic growth model, such as the generalized logistic equation and the Gompertz equation, can provide a more accurate representation of the data.
Generalized Logistic Equation
The generalized logistic equation is a flexible extension of the standard logistic equation that allows for a wider range of growth patterns. It is given by the equation:
$$P(t) = \fracK[1 + Ae^-rt]^1/m$$
where Kis the carrying capacity, ris the intrinsic growth rate, Ais a parameter that determines the initial growth rate, and mis a shape parameter that controls the curvature of the growth curve.
The generalized logistic equation can capture a variety of growth patterns, including sigmoidal curves with different degrees of curvature, as well as curves with an initial lag phase or a period of decline followed by recovery.
Gompertz Equation
The Gompertz equation is another extension of the logistic growth model that is often used to describe the growth of populations that experience a constant relative growth rate. It is given by the equation:
$$P(t) = Ke^-ae^-rt$$
where Kis the carrying capacity, ris the intrinsic growth rate, and ais a parameter that determines the initial growth rate.
The Gompertz equation produces a growth curve that is initially exponential, but gradually slows down and approaches the carrying capacity asymptotically. This pattern is commonly observed in the growth of biological populations, such as bacteria or cancer cells.
Expert Answers
What is the significance of logistic growth in population modeling?
Logistic growth accurately represents the limited resources available in real-world environments, leading to a carrying capacity that prevents exponential population growth.
How can I determine the carrying capacity of a population using the logistic growth equation?
The carrying capacity, K, is a parameter in the logistic growth equation that represents the maximum population size sustainable in a given environment.
What is the inflection point of a logistic growth curve?
The inflection point marks the transition from exponential growth to a slower growth rate as the population approaches its carrying capacity.