Unit 11 test study guide volume and surface area – Unit 11 Test Study Guide: Volume and Surface Area embarks on an enlightening journey, unraveling the intricacies of these fundamental concepts that shape our physical world. Delving into the depths of geometry, this guide illuminates the relationship between volume and surface area, their practical applications, and effective study strategies.
Volume, a measure of the three-dimensional space occupied by an object, and surface area, the measure of its external boundaries, play pivotal roles in various fields, from architecture to biology. Understanding these concepts is essential for comprehending the world around us and solving real-world problems.
Understanding Volume and Surface Area
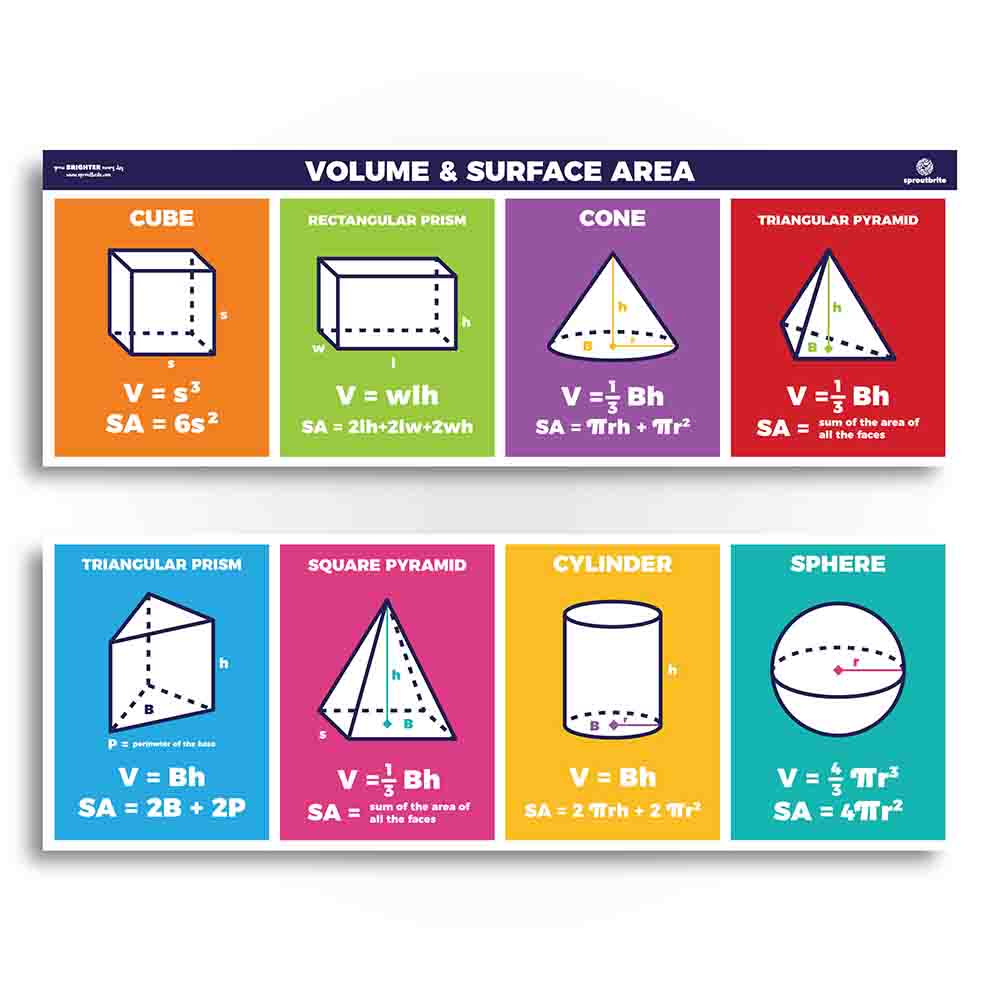
Volume is the amount of three-dimensional space occupied by an object, while surface area is the total area of the object’s surfaces. Volume is measured in cubic units, such as cubic centimeters (cm 3) or cubic meters (m 3), while surface area is measured in square units, such as square centimeters (cm 2) or square meters (m 2).
The relationship between volume and surface area is that the surface area of an object is directly proportional to its volume. This means that as the volume of an object increases, so does its surface area.
Examples of Real-Life Applications of Volume and Surface Area
- Architecture and engineering:Volume is used to calculate the size of buildings and other structures, while surface area is used to calculate the amount of materials needed to build them.
- Biology and chemistry:Volume is used to measure the size of cells and other biological structures, while surface area is used to calculate the rate of chemical reactions.
- Everyday life:Volume is used to measure the amount of liquid in a container, while surface area is used to calculate the amount of paint needed to cover a wall.
Measuring Volume and Surface Area

The formulas for calculating volume and surface area vary depending on the shape of the object. For example, the formula for the volume of a cube is V = a 3, where a is the length of one side of the cube.
The formula for the surface area of a cube is A = 6a 2.
To use the formulas to solve problems, simply plug in the values for the given dimensions of the object. For example, to find the volume of a cube with a side length of 5 cm, you would plug in a = 5 into the formula V = a 3, which would give you a volume of 125 cm 3.
Using Geometric Shapes to Calculate Volume and Surface Area
Geometric shapes can be used to calculate the volume and surface area of objects. For example, the volume of a cylinder can be calculated using the formula V = πr 2h, where r is the radius of the base of the cylinder and h is the height of the cylinder.
The surface area of a cylinder can be calculated using the formula A = 2πr(r + h).
Applications of Volume and Surface Area: Unit 11 Test Study Guide Volume And Surface Area
Volume and surface area are used in a variety of applications, including architecture, engineering, biology, and chemistry.
Architecture and Engineering
In architecture and engineering, volume is used to calculate the size of buildings and other structures, while surface area is used to calculate the amount of materials needed to build them. For example, an architect might use volume to calculate the size of a room, while an engineer might use surface area to calculate the amount of paint needed to cover a wall.
Biology and Chemistry
In biology and chemistry, volume is used to measure the size of cells and other biological structures, while surface area is used to calculate the rate of chemical reactions. For example, a biologist might use volume to measure the size of a cell, while a chemist might use surface area to calculate the rate of a chemical reaction.
Volume and Surface Area of Irregular Objects

The volume and surface area of irregular objects can be calculated using a variety of methods, including the water displacement method, the geometric approximation method, and the 3D scanning method.
Water Displacement Method
The water displacement method is a simple method for calculating the volume of an irregular object. To use this method, you simply submerge the object in a container of water and measure the amount of water that is displaced. The volume of the object is equal to the amount of water that is displaced.
Geometric Approximation Method
The geometric approximation method is a method for calculating the volume and surface area of an irregular object by approximating it with a regular geometric shape. For example, you might approximate the volume of a rock by approximating it with a sphere.
The volume of the sphere would then be an approximation of the volume of the rock.
3D Scanning Method, Unit 11 test study guide volume and surface area
The 3D scanning method is a method for calculating the volume and surface area of an irregular object using a 3D scanner. A 3D scanner is a device that creates a digital model of an object by scanning its surface.
The digital model can then be used to calculate the volume and surface area of the object.
Strategies for Studying Volume and Surface Area
There are a number of strategies that you can use to study volume and surface area effectively.
- Understand the concepts:Make sure that you understand the concepts of volume and surface area before you start trying to solve problems.
- Memorize the formulas:Memorize the formulas for calculating volume and surface area. This will make it easier for you to solve problems.
- Practice solving problems:The best way to learn how to solve volume and surface area problems is to practice. Solve as many problems as you can find.
Detailed FAQs
What is the relationship between volume and surface area?
Volume measures the three-dimensional space occupied by an object, while surface area measures its external boundaries. In general, as the volume of an object increases, its surface area also tends to increase.
How can I calculate the volume of a rectangular prism?
To calculate the volume of a rectangular prism, multiply its length, width, and height. For example, if a prism has a length of 5 cm, a width of 3 cm, and a height of 2 cm, its volume would be 5 cm x 3 cm x 2 cm = 30 cubic centimeters.
What are some real-life applications of volume and surface area?
Volume and surface area have numerous applications in various fields. For instance, in architecture, they are used to calculate the space and materials required for buildings. In biology, they are used to determine the size and shape of cells and organisms.
In chemistry, they are used to calculate the volume and surface area of molecules.


