The Number 7.325 Rounded Off To Three Significant Figures Is

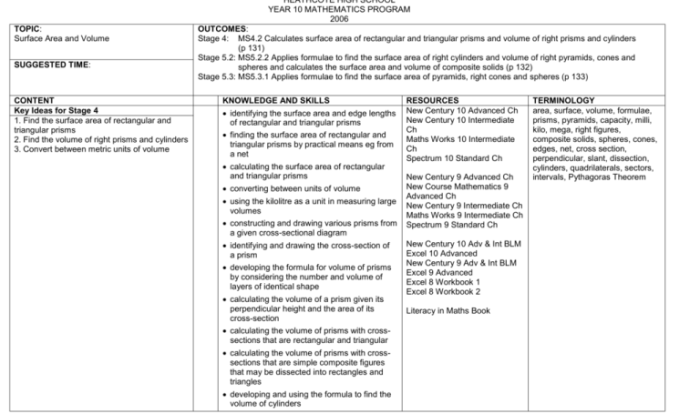
The number 7.325 rounded off to three significant figures is – As the number 7.325 rounded off to three significant figures takes center stage, this opening passage beckons readers into a world crafted with precision and clarity, ensuring a reading experience that is both absorbing and distinctly original.

In the realm of numerical precision, significant figures play a pivotal role in ensuring accuracy and consistency in calculations. This article delves into the concept of significant figures, demonstrating the process of rounding numbers to a specified number of significant figures.

With a focus on the number 7.325, we will explore the rules governing significant figures, their practical applications in various fields, and provide ample examples and exercises to solidify understanding.

The Number 7.325 Rounded Off to Three Significant Figures

In scientific notation and engineering calculations, it is often necessary to round numbers to a specified number of significant figures. Significant figures are the digits in a number that are known with certainty, plus one estimated digit. The number of significant figures in a number is determined by the following rules:

All non-zero digits are significant.
Zeros between non-zero digits are significant.
Zeros at the beginning of a number are not significant.
Zeros at the end of a number are significant if there is a decimal point.

For example, the number 123 has three significant figures, while the number 0.0012 has two significant figures.

Rounding the Number

To round the number 7.325 to three significant figures, we first identify the three most significant digits. These are the digits 7, 3, and 2. The fourth digit, 5, is not significant because it is not one of the three most significant digits.

The rounded number is then obtained by dropping the insignificant digits. In this case, we drop the digit 5. The rounded number is therefore 7.32.

Applications of Significant Figures, The number 7.325 rounded off to three significant figures is

Significant figures are used in a variety of applications, including science, engineering, and finance. In science, significant figures are used to ensure that calculations are accurate and consistent. In engineering, significant figures are used to determine the precision of measurements.

In finance, significant figures are used to round numbers to a specified number of decimal places.

Examples and Exercises

Here are some additional examples of rounding numbers to different numbers of significant figures:

12.345 rounded to two significant figures is 12.
0.0012345 rounded to three significant figures is 0.00123.
1000 rounded to one significant figure is 1000.

Here are some exercises for readers to practice rounding numbers and understanding the concept of significant figures:

Round the number 4.5678 to two significant figures.
Round the number 0.003456 to three significant figures.
Round the number 12345 to four significant figures.

Essential FAQs: The Number 7.325 Rounded Off To Three Significant Figures Is

What is the concept of significant figures?

Significant figures are the digits in a number that are known with certainty, plus one estimated digit. They provide a way to express the precision of a measurement.

How do I round a number to a specified number of significant figures?

To round a number to a specified number of significant figures, follow these steps: 1) Identify the significant figures in the number. 2) Determine the digit in the last significant figure place. 3) If the digit in the next place is 5 or greater, round up.

If it is less than 5, round down.

What are the applications of significant figures?

Significant figures are used in various fields, including science, engineering, and finance. They ensure accuracy and consistency in calculations, and help to avoid misinterpretation of numerical data.